Bachelor Semester Project
Speeding up the Quantification of Data Staleness in Dynamic Bayesian Optimization
Full Report: HERE Main Paper: HERE
In the third year of Bachelor at EPFL you have to find a semester project in a laboratory. I chose to go in the lab of one of my favorite professor (Prof. Patrick Thiran), and found an interesting topic: Dynamic Bayesian Optimization (DBO). Its an extention of Bayesian Optimization (BO) to time-varying fucntions. The idea is to optimize a function without knowing its functional form, leaving gradient-descent methods for example useless. My project involved understanding a new algorithm developed by my supervisor Anthony Bardou called W-DBO. It uses a criterion that quantifies how relevant an observation is for the future predictions of the Gaussian Process, the main concept used by the BO framework. The goal of the project has been to (i) implement the criterion in C++ and calling it using Python bindings, (ii) evaluate the performance of this implementation compared to a Python implementation, (iii) evaluate the performance of W-DBO compared to the state of the art.
Additionally, we develop Python packages for W-DBO and the criterion!
The core of the project
By evolving in time, the optimum of the function changes, and observations of the function become less relevant due to their lack of information on its future values. In a long-period time optimization, keeping all of them will impact the performance of BO. In fact, the sampling frequency will decrease due to the growth of the Gaussian Process’ inference time. For people knowing Gaussian Processes, conditioning it with a new observation does not change the distribution, leaving this method very useful for calculations. To remove them rapidly, the criterion should be calculated efficiently in a low-level programming language.
Results
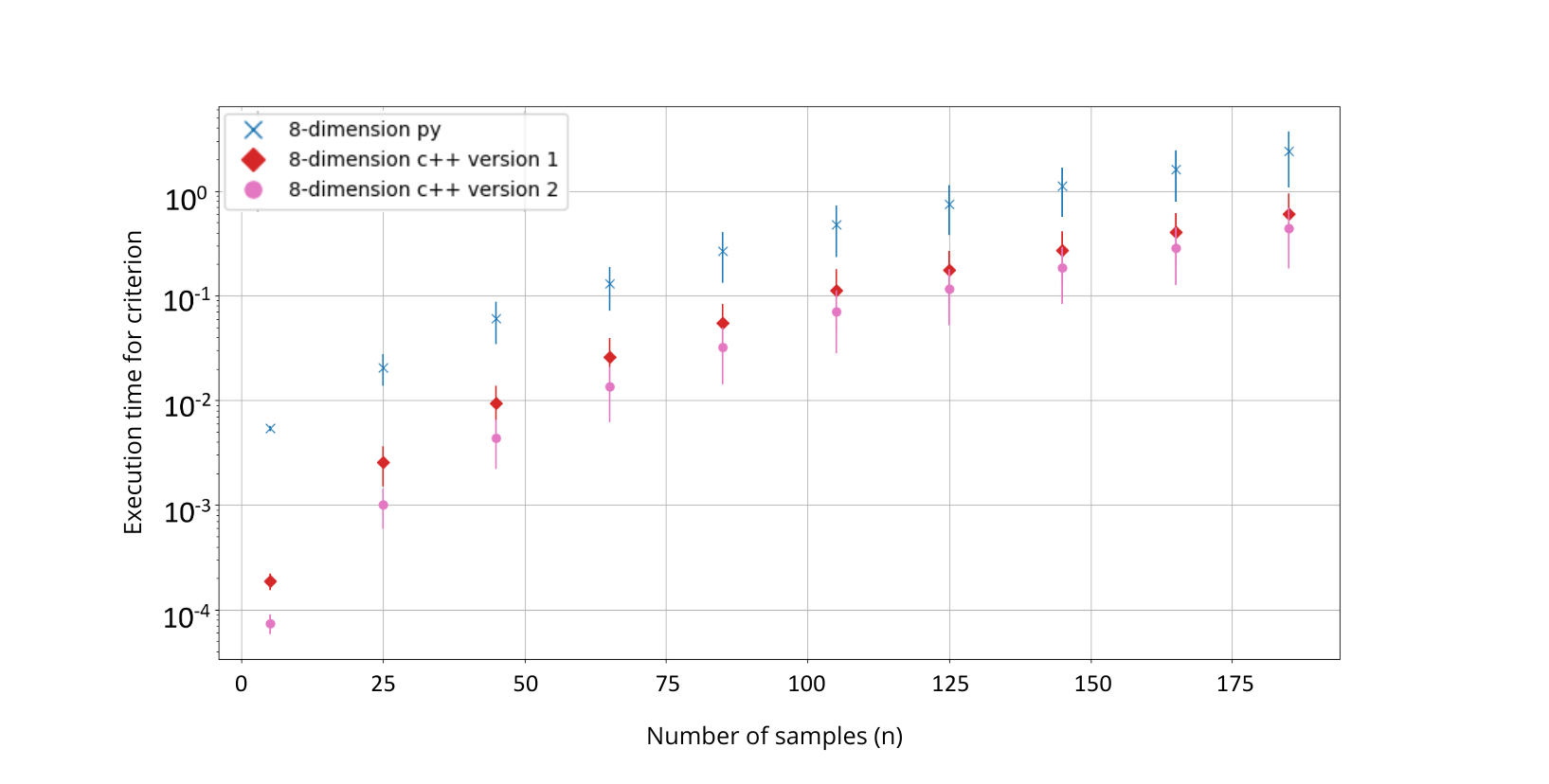
By speeding up the computations using C++ to calculate the criterion, W-DBO shown great improvements over state of the art solutions. The idea has been to follow the main paper introducing W-DBO and solving the equations in the code using the linear algebra library Eigen3. I really enjoyed implementing maths in C++, because it has been the first time where you understand that implementing mathematical stuff is not easy. Take for example derivatives, how do you compute them without a closed-form? Or inverting a matrix efficiently?
The first question was solved using a very simple class for differentiation, using the concept of auto-differentiation. You start with a complicated function and you break it down using the basic laws of differentiation (products, sums, constants, etc). I had the chance to have functions not too complicated, but still involving many types of products, etc. The second question was answered case by case. Most of my matrices where positive semi-definite (PSD), giving cool properties for speeding up computations. You will find everything in my report if you are interested in these problem-solving concepts.
In the end, I got this following graph, where we see the optimization that I’ve done to compute the criterion.